22. Riemann Sums, Integrals and the FTC
Recall, in general: \(\displaystyle \int_a^bf(x)\,dx =\lim_{\begin{aligned}&\scriptstyle\quad n\to\infty \\ &\scriptstyle\text{max}\Delta x_i\to0\end{aligned}} \sum_{i=1}^n f(x_i^*)\Delta x_i\) where \(\Delta x_i=x_i-x_{i-1}\) and \(x_i^*\in[x_{i-1},x_i]\). For equal intervals and right endpoints: \(\displaystyle \int_a^bf(x)\,dx =\lim_{n\to\infty} \sum_{i=1}^n f(x_i)\Delta x\) where \(\Delta x=\dfrac{b-a}{n}\) and \(x_i=a+i\Delta x\).
a3. Limits of Riemann Sums (Optional)
So far, we have approximated integrals using equal intervals with right endpoints, or left endpoints or midpoints. We now discuss how to actually compute the integrals by taking the limits. We will do this by example and restrict to polynomial integrands and use equal intervals and right endpoints.
We first recall some basic summation formulas from high school algebra or pre-calculus.
\[\begin{aligned} \sum_{i=1}^n 1 &=n &\sum_{i=1}^n i &=\dfrac{n(n+1)}{2} \\ \sum_{i=1}^n i^2 &=\dfrac{n(n+1)(2n+1)}{6} \qquad &\sum_{i=1}^n i^3 &=\dfrac{n^2(n+1)^2}{4} \end{aligned}\] These are proved using Mathematical Induction.
Compute the integral \(\displaystyle \int_1^3 x^3-6x\,dx\) as a limit of Riemann sums.
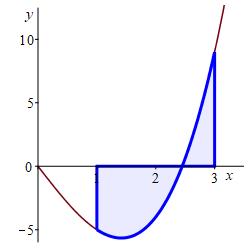
We split the interval \([1,3]\) into \(n\) equal parts of width: \[ \Delta x=\dfrac{3-1}{n}=\dfrac{2}{n} \] Then the right endpoints are: \[ x_i=1+i\Delta x=1+\dfrac{2}{n}i \] Since the integrand is the function \(f(x)=x^3-6x\), its value at a right endpoint is: \[\begin{aligned} f(x_i)&=(x_i)^3-6(x_i) =\left(1+\dfrac{2}{n}i\right)^3-6\left(1+\dfrac{2}{n}i\right) \\ &=1+3\dfrac{2}{n}i+3\dfrac{2^2}{n^2}i^2+\dfrac{2^3}{n^3}i^3-6-\dfrac{12}{n}i \\ &=-5-\dfrac{6}{n}i+\dfrac{12}{n^2}i^2+\dfrac{8}{n^3}i^3 \end{aligned}\] We set up the Riemann sum, expand each term, write it as a sum of summations and factor out the coefficients: \[\begin{aligned} \sum_{i=1}^n &f(x_i)\Delta x =\sum_{i=1}^n \left[\left(1+\dfrac{2}{n}i\right)^3-6\left(1+\dfrac{2}{n}i\right)\right]\dfrac{2}{n} \\ &=\sum_{i=1}^n \left(-5-\dfrac{6}{n}i+\dfrac{12}{n^2}i^2+\dfrac{8}{n^3}i^3\right) \dfrac{2}{n} \\ &=\sum_{i=1}^n \left(-\dfrac{10}{n}-\dfrac{12}{n^2}i +\dfrac{24}{n^3}i^2+\dfrac{16}{n^4}i^3\right) \\ &=\sum_{i=1}^n \dfrac{-10}{n}+\sum_{i=1}^n \dfrac{-12}{n^2}i +\sum_{i=1}^n \dfrac{24}{n^3}i^2+\sum_{i=1}^n \dfrac{16}{n^4}i^3 \\ &=-\,\dfrac{10}{n}\sum_{i=1}^n 1-\dfrac{12}{n^2}\sum_{i=1}^n i +\dfrac{24}{n^3}\sum_{i=1}^n i^2+\dfrac{16}{n^4}\sum_{i=1}^n i^3 \end{aligned}\] We now use the basic summations and simplify: \[\begin{aligned} \sum_{i=1}^n &f(x_i)\Delta x \\ &=-\,\dfrac{10}{n}\cdot n-\dfrac{12}{n^2}\cdot\dfrac{n(n+1)}{2} +\dfrac{24}{n^3}\cdot\dfrac{n(n+1)(2n+1)}{6} +\dfrac{16}{n^4}\cdot\dfrac{n^2(n+1)^2}{4} \\ &=-10-6\dfrac{(n+1)}{n} +4\dfrac{(n+1)(2n+1)}{n^2} +4\dfrac{(n+1)^2}{n^2} \\ \end{aligned}\] Finally, we compute the integral as the limit of this Riemann sum: \[\begin{aligned} \int_1^3 &x^3-6x\,dx =\lim_{n\to\infty}\sum_{i=1}^n f(x_i)\Delta x \\ &=\lim_{n\to\infty}\left(-10-6\dfrac{(n+1)}{n} +4\dfrac{(n+1)(2n+1)}{n^2}+4\dfrac{(n+1)^2}{n^2}\right) \\ &=-10-6+8+4=-4 \end{aligned}\]
Compute the integral \(\displaystyle \int_1^9(x^2+1)\,dx\) as a limit of Riemann sums.
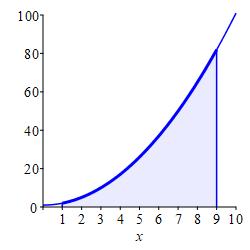
\(\displaystyle \int_1^9(x^2+1)\,dx=\dfrac{752}{3} \approx250.67\)
We split the interval \([1,9]\) into \(n\) equal parts of width: \[ \Delta x=\dfrac{9-1}{n}=\dfrac{8}{n} \] Then the right endpoints are: \[ x_i=1+i\Delta x=1+\dfrac{8}{n}i \] Since the integrand is the function \(f(x)=x^2+1\), its value at each right endpoint is: \[\begin{aligned} f(x_i)&=(x_i)^2+1=\left(1+\dfrac{8}{n}i\right)^2+1 \\ &=2+\dfrac{16}{n}i+\dfrac{64}{n^2}i^2 \end{aligned}\] We set up the Riemann sum, expand each term, write it as a sum of summations and factor out the coefficients: \[\begin{aligned} \sum_{i=1}^n &f(x_i)\Delta x =\sum_{i=1}^n \left[\left(1+\dfrac{8}{n}i\right)^2+1\right]\dfrac{8}{n} \\ &=\sum_{i=1}^n \left(2+\dfrac{16}{n}i+\dfrac{64}{n^2}i^2\right)\dfrac{8}{n} \\ &=\sum_{i=1}^n \left(\dfrac{16}{n}+\dfrac{128}{n^2}i+\dfrac{512}{n^3}i^2\right) \\ &=\sum_{i=1}^n \dfrac{16}{n}+\sum_{i=1}^n \dfrac{128}{n^2}i +\sum_{i=1}^n \dfrac{512}{n^3}i^2 \\ &=\dfrac{16}{n}\sum_{i=1}^n 1+\dfrac{128}{n^2}\sum_{i=1}^n i +\dfrac{512}{n^3}\sum_{i=1}^n i^2 \\ \end{aligned}\] We now use the basic summations and simplify: \[\begin{aligned} \sum_{i=1}^n &f(x_i)\Delta x \\ &=\dfrac{16}{n}\cdot n+\dfrac{128}{n^2}\cdot\dfrac{n(n+1)}{2} +\dfrac{512}{n^3}\cdot\dfrac{n(n+1)(2n+1)}{6} \\ &=16+64\dfrac{(n+1)}{n} +\dfrac{256}{3}\dfrac{(n+1)(2n+1)}{n^2} \\ \end{aligned}\] Finally, we compute the integral as the limit of this Riemann sum: \[\begin{aligned} \int_1^9 &x^2=1\,dx =\lim_{n\to\infty}\sum_{i=1}^n f(x_i)\Delta x \\ &=\lim_{n\to\infty}\left(16+64\dfrac{(n+1)}{n} +\dfrac{256}{3}\dfrac{(n+1)(2n+1)}{n^2}\right) \\ &=16+64+\dfrac{512}{3}=\dfrac{752}{3} \approx250.67 \end{aligned}\]
In a remark on an exercise on the previous page the correct value of the integral: \[ \int_1^9(x^2+1)\,dx=\dfrac{752}{3}\approx250.67 \] was compared to the left, midpoint and right Riemann sum approximations to the integral: \[ L_8=212 \quad M_8=250 \quad R_8=292 \] Since the function is increasing, the left sum is too small, the right sum is too large and the middle sum is just about right. (Papa Bear, Momma Bear and Baby Bear.)
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum